LeetCode 110. Balanced Binary Tree

LeetCode 110. Balanced Binary Tree

Problem Description

Given a binary tree, determine if it is height-balanced.

A height-balanced binary tree is a binary tree in which the height of the two subtrees of any node is not more than 1.

The height of a tree is defined as the length of the longest path from the root node to any leaf node in the tree. This length is usually measured as the number of edges along that path. (Other defintions may mention the number of nodes along that path)

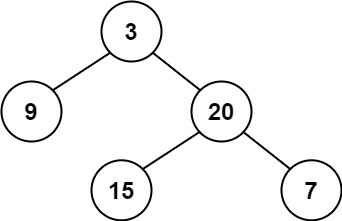
Example 1:

Output: True

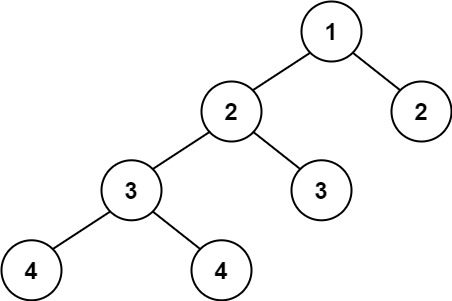
Example 2:

Output: False

Approach

To determine if the tree is height-balanced, we can check if for every node, the height of its two subtrees is less than or equal to 1. If this is satisfied for every node, then the tree is height-balanced.

To that end, first we need a helper method to find the height of a tree. We can recursively find the height of a tree.

BASE CASE: if the tree is empty, its height is zero.

RECURSIVE CASE: if the tree is not empty, then its height is one more than the maximum of the heights of its left and right subtrees.

With this helper function, we will check if every subtree is height balanced. We will check it for the current node and then recurse down to the left and right subtrees.

Note: You can also precompute the heights of every subtree with a single run of DFS so that you don’t have to call getHeight(root) for every node.

Code

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;

        int leftSubtreeHeight = getHeight(root.left);
        int rightSubtreeHeight = getHeight(root.right);

        return Math.abs(leftSubtreeHeight - rightSubtreeHeight) <= 1
        && isBalanced(root.left) && isBalanced(root.right);   
    }


    int getHeight(TreeNode root){
        if(root == null) return 0;
        return 1 + Math.max(getHeight(root.left), getHeight(root.right));
    }

}